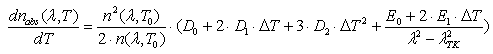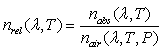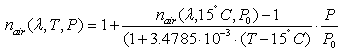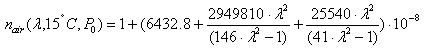|
Temperature Coefficient of Refractive Index (dn/dT) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
The refractive index of optical glass changes with the temperature. The change is given by:
where
The refractive index values given in the optical glass catalog apply for an air pressure of 101.33 kPa. They are called relative refractive index values (nrel ). These values can be used for n(λ,T0) in equation (1) with sufficient accuracy. The refractive index relative to air nrel(λ,T0) can be calculated from:
where
With the help of 6 glass specific parameters D0, D1, D2, E0, E1 and λTK, the value of the temperature coefficient of the absolute refractive index (compared to vacuum) as a function of temperature and wavelength can be calculated with equation (1) for each glass type. The corresponding value for air can be calculated by (2).
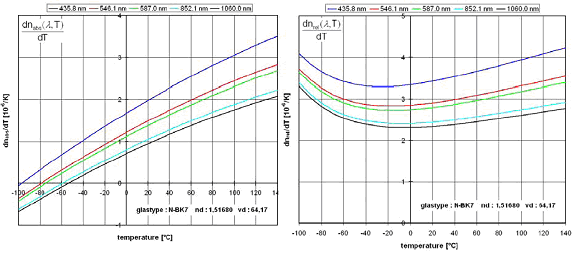
The following figure shows the change of the temperature coefficients of N-BK7 refractive index (absolute on the left side and relative on the right side) with temperature for different wavelengths. It can be seen that the shape of the curve of the relative temperature coefficients differs from the absolute temperature coefficients. The reason is the influence of the temperature coefficients of the air. In general the temperature influence on the refractive index at shorter wavelength compared to longer wavelength is much higher.
Properties:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Copyright © 2016 Precision Micro-Optics Inc. All Rights Reserved.